Database Design: Avoid Derivative State

This is the beginning of a potential series on effective database design.

Before we get into the nitty-gritty, let’s address the elephant in the room: what is derivative state? I haven’t heard this term being used elsewhere so I’m going to officially define it here as:

Derivative state is state that can be derived from another piece of state (the parent state). By definition, this means the derived state cannot carry more information than its parent. In other words, it is either less or equally informative as its parent state.

This probably sounds very abstract right now so let’s try to reify the concept by presenting an example, diving into information theory, then bringing it all together with a couple possible solutions.

Let’s start with an example.

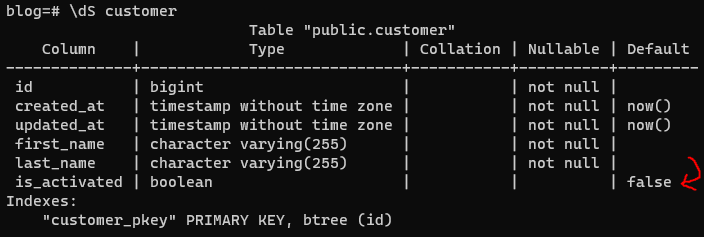
I spend a lot of time working with databases and I see a lot of this:

which roughly translates to this DAO generated from an ORM library:

public class Customer {

    private long id;

    private Timestamp createdAt;

    private Timestamp updatedAt;

    private String firstName;

    private String lastName;

    private boolean isActivated;

    public boolean isActivated() {
        return this.isActivated;
    }

    // other methods
}

The rest of this post will focus on the boolean isActivated field; specifically, I’m going to argue that derivative state should be avoided in database design by examining the simplest piece of derivative state: booleans. I will attempt to show that derivative state leads to design and data smells, then use those same ideas to argue for avoiding derivative state in general.

Let’s start with a boolean. Why are they derivative and why could that be a smell?

1. Information theory tells us a boolean wastes almost all of the information in its representation.
2. Good design tells us a boolean is almost always derivative state and can be derived from something more informative.

Information Theory

Information theory defines entropy as a variable that is a measure of “information” inherent in the variable’s possible outcomes. Computer scientists use Shannon’s entropy equation as a measure of entropy:

This equation states that for a variable X with possible outcomes x1, … ,xn, each of which have a probability P(xi), then the entropy of X is defined as the sum of the product of the probability of a single outcome and its logarithm. The base of the logarithm that you use defines the output unit of the equation. If you use a base of 2, then we get “bits” as the unit of measurement – this is certainly convenient for us as software engineers. As the entropy of a system reaches 0 bits, this indicates the system doesn’t provide any information; inversely, an increasing entropy means that there is more “information” in the outcome.

Let’s try to understand the equation with an extreme example. Suppose that we have a super unfair coin where both sides of the coin is a head; this means that the chance of getting heads on any coin toss is 100% and 0% for getting tails. If we plug these numbers into the equation (x1 = heads, x2 = tails, P(x1) = 1.0, P(x2) = 0.0), then we get an entropy of 0 bits. This means that any outcome of this unfair coin provides us no new information. It makes sense if you think about it: since we know the coin is unfair and will always return heads, we don’t gain anything out of tossing the coin any number of times; we know the coin will always return heads and our coin toss experiments will not provide us any additional context to change that assertion. Therefore, there is no new information to be gained here.

With that in mind, let’s use the equation to measure the entropy of a boolean; a boolean only has two states – true or false – meaning that x1 = true and x2 = false. Without further context, we have no choice but to assume an equal probability of either outcome so we say that P(x1) = 0.5 and P(x2) = 0.5. If you plug all of this information into the equation, you get exactly 1 bit of entropy:

Consider that most programming languages implement a boolean as a 1 byte (8 bit) entity (mostly due to the CPU’s inability to address less than 1 byte at a time), we see that the total amount of utilized information in a boolean is 1 / 8 or ~12.5%. In other words, 87.5% of the total information a boolean can hold is wasted.

It gets worse though. Earlier, we assumed that the probability of either true or false is 0.5. This is almost certainly a false assumption in the real world. In our case with the isActivated field, isActivated will probably be either false for a long time (if the user didn’t take the time to activate) or true for a long time (if the user took the time to activate right away). This means that the probabilities are closer to being something like 0.9 and 0.1. If we plug those values into our equation, we get 0.47 bits of entropy – even less information than before!

State Design

So we’ve shown that a boolean is a very wasteful representation. How can we do better?

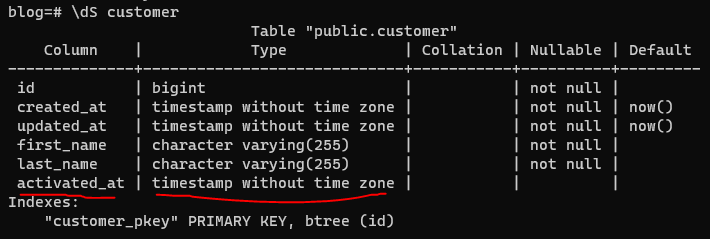
Consider this change:

public class Customer {

    private long id;

    private Timestamp createdAt;

    private Timestamp updatedAt;

    private String firstName;

    private String lastName;

    private Timestamp activatedAt;

    public boolean isActivated() {
        return this.activatedAt != null;
    }

    // other methods
}

We swapped the boolean field for a Timestamp holding the time the user was activated and we introduce a boolean method instead that implements the isActivated logic.

Now we see the derivative nature of booleans. We were able to derive the boolean state from a Timestamp by saying that the Customer is activated if the activatedAt field is not null. In other words, the value of isActivated depends on the value of activated_at. We won’t go into the calculations to show the entropy of a Timestamp here but if you think about it, it isn’t too difficult to arrive at the conclusion that a Timestamp has much more entropy – and thus much more information – than a boolean.

You may be asking yourself at this point:

So what? Who cares? Why is this practically useful?

After all, us software engineers take great pride in being practical people. Here are some considerations:

1. Ask yourself when the last time just knowing if something happened was all product owners needed to know.
   • In my experience, product managers want to know when something happened or what happened.
2. From a development point of view, it’s easy to get state with less information out of more state with more information.
   • Take the above example. How easy was it to implement isActivated given activatedAt?
   • Think about how much more difficult it could be to implement activatedAt when all you have is isActivated.

This pattern isn’t specific to booleans and Timestamps either. Let’s conclude with one more example.

Imagine if we wanted to extend Customer so that we knew how many Orders a customer put through. If we extended Customer to have a list of Orders, then getting that information would be trivial. Imagine if we instead put an int orderCount field on Customer. While getting the number of orders would still be trivial (a simple getter method), maintaining the orderCount invariant in Customer would be more difficult and error prone than with a listing of the Orders. Instead of just appending or removing an Order from the list of orders to represent adding or removing an order, we now have to ensure that we increment/decrement the orderCount field anywhere we update the orders on the Customer.